Puno lipih stvari u novoj verziji mog matematičkog librarya za C++, i planirani scope se pred verziju 1.0 polako zaokružuje. Već se doduše vidi da u idućem dvotjednom sprintu nema šanse da stignem pozavršavati što je bilo originalno planirano 🤣, ali ono glavno će se ipak stići 💪.

Glavni fokus u ovoj verziji (iliti executive summary odrađenoga) – značajno poboljšanje vizualizacije parametarskih krivulja, sada i sa mogućnošću animacije (vidi video niže u postu); dovršetak implementacije surface integration s prikladnim ekstenzijama u geometry 3D modulu (s čime sam polako zaokružio numeričke alate potrebne za vektorsku analizu); kreirane klase Serializer i Visualizer, i proveden refactoring kako bi bile single-point-of-implementation za svoje domene (a i olakšava put ka cross-platform vizualizaciji), te dorađena TablePrinter klasa (za vizualizaciju u konzoli); implementiran GravitySimulator primjer uz dinamičku vizualizaciju putanje; proširen README i (ponešto) dorađeni docs.

To bi bilo onako ukratko.

Poboljšanja u implementaciji ParametricCurve3Vizualizera su zaslužna što ovaj post ima i par lijepih slika. Prvo poboljšanje je mogućnost da se istovremeno prikaže više krivulja, a što je recimo zgodno kod uspoređivanja različitih rješenja diferencijalnih jednadžbi pa je tako na donjoj slici prikazana ljepota Lorentzovog (kaotičnog) atraktora kroz vizualizaciju rješenja Lorentzove diferencijalne jednadžbe za pet različitih početnih uvjeta.

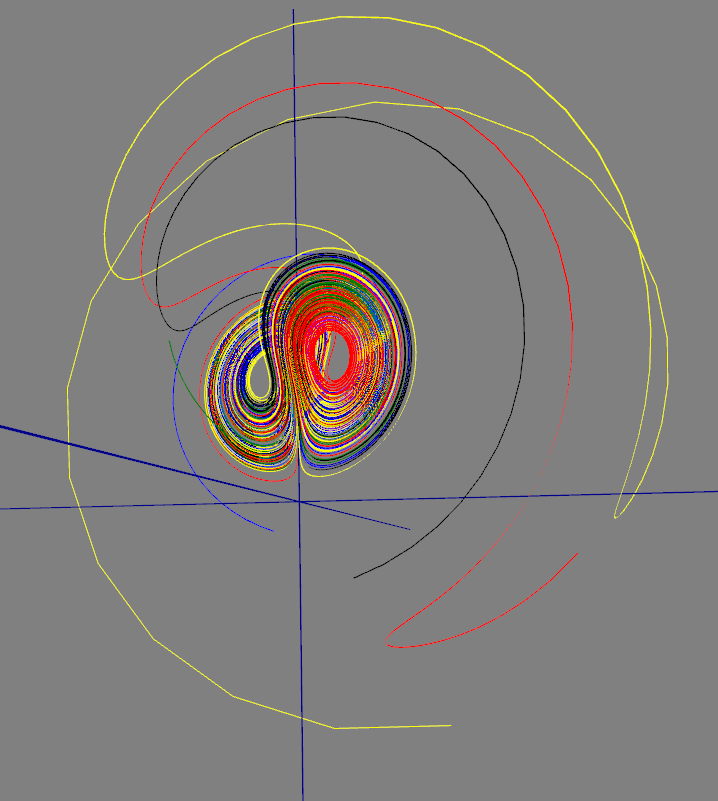
Mislim da dosta dobro prikazuje zašto se to zove “atraktor” 😎. (za one koji su malo manje potkovani u diferencijalnim jednadžbama, ključna stvar za uočiti su dosta različite početne točke ovih krivulja, a koje odgovaraju različitim početnim uvjetima, a koje sve vrlo brzo završe u istom atraktoru).

Drugo zanimljivo poboljšanje je mogućnost dinamičkog simuliranja parametarskih krivulja, na način da se ne prikazuju kompletne trajektorije (od nekog t0, do nekog t1), već da se prikaže kretanje neke male sfere, po danoj trajektoriji, dinamički u vremenu.

Savršeno za vizualizaciju Gravity simulatora 😎.

Ni sam simulator nije previše kompliciran, a setup za simulaciju je pogotovo jednostavan.

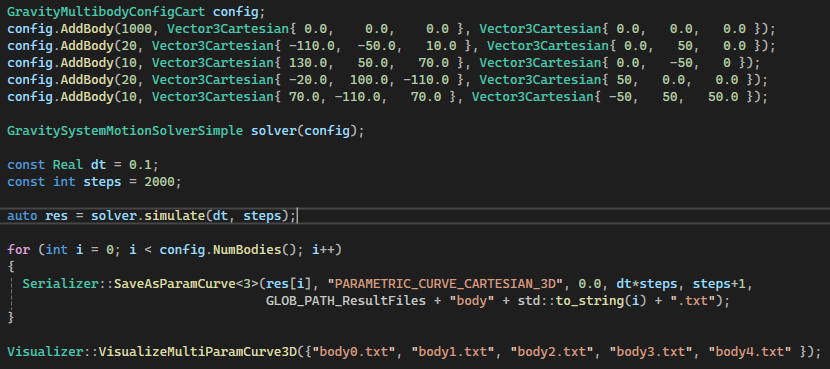
Ovo je vizulizacija kompletnih krivulja trajektorija tih pet tijela, dobivena simulacijom.

Statička slika ne daje najbolji pregled, pa evo i video s 3D pregledom ovih krivulja, da se vidi odnos tih krivulja u prostoru (nažalost, dosta loše kvalitete 🤔).

I za kraj, video s dinamičkim prikazom gibanja tijela (posebnu pozornost obratite na crvenu kuglu).

Vizualizacijski dio je time zaokružen u svojim osnovama (naravno, ima tisuću potencijalnih malih poboljšanja!), a druga bitna stvar u ovoj verziji je surface integration … kad se želim poigrati s elektrodinamikom, Stokesovim zakonom, mogućnost računanja fluksa (toka) elektromagnetskog polja je nužnost.

U implementacijskom smislu, stvar se ponajviše svodi na načine modeliranja površina i tijela, jer su sami algoritmi ne trivijalni, ali suštinski jednostavni, te promišljanja o preciznosti i točnosti.

Eh da, skoro zaboravih – u ovoj verziji dolazi i FunctionAnalyzer klasa i koja me u tom pogledu posebno veseli – kako numerički implementirati kriterije neprekidnosti funkcije … deep rabbit hole, ako želiš apsolutnu istinu 🤣 (što je put koji mene ne zanima jer je možda i najvažnija lekacija cijele ove implementacije MML-a da je napisati matematički library koji će out-of-the-box zadovoljavati potrebe svakog korisnika, a da taj korisnik ne mora dubinski promisliti o problemu koji rješava, potpuno nemoguća misija).

No, zato su sve moje funkcije “pošpricane” s Real defEps=1-e6 zadnjim parametrom, pa korisnik uvijek ima opciju (pri čemu MML ima i DefaultsPrecision statičku klasu, a imam i ideja kako hendlanje preciznosti tijekom korištenja različitih algoritama učiniti što jednostavnijim, no to je ipak za budućnosti).

Malo još dovršiti tenzore ❤️, dovršiti CoordSystems i kosi hitac primjer, poigrati se sa FunctionSpace i LinearOperator (da se odradi i štogod algebre), proračunati elektromagnetski tenzor za danu konfiguraciju naboja i struja … i to je to, plan za 1.0.

• IT
• Osobno